## Import the dataset
osterman <- data_read("https://cgmoreh.github.io/HSS8005/data/osterman_t3.dta")
## Set a seed for being able to reproduce the random sampling in the next step
set.seed(1234)
## Select countries and keep 50 respondents per country at random
osterman <- osterman %>%
filter(cntry %in% c("GB", "IE", "DE", "FR", "HU", "PL", "PT", "ES")) %>%
group_by(cntry) %>% slice_sample(n=50) %>% ungroup() Week 5
Hierarchies
Hierarchical data structures and multilevel modelling
Description
Hierarchical data are ubiquitous in the social and human sciences (and beyond). In fact, almost all the application articles we have engaged with so far in previous labs modelled hierarchical data., and almost all modelled them explicitly as such, applying some multilevel modelling technique. In some cases the hierarchies themselves were of central theoretical importance and played a crucial role in the stated estimand (i.e. the object of inquiry—(…) the precise quantity about which we marshal data to draw an inference
(see Lundberg, Johnson, and Stewart 2021:532). In others, taking into account the hierarchical nature of the data was meant to improve the precision of the main effect estimates. The importance of accounting for hierarchical dependencies in our models is emphasised by no one else more than Richard McElreath, who, in his important introductory-level book to Bayesian statistics, wants to convince the reader of something that appears unreasonable: multilevel regression deserves to be the default form of regression
(McElreath 2020:15). According to him, papers that do not use multilevel models should have to justify not using a multilevel approach
. In this session, we will learn how to think about and fit hierarchical models in R, and we’ll discuss some of the challenges of multilevel modelling and the possible justifications not to use them in certain contexts.
Readings
Textbook
Application
- Österman, Marcus. 2021.
Can We Trust Education for Fostering Trust? Quasi-Experimental Evidence on the Effect of Education and Tracking on Social Trust
. Social Indicators Research 154(1):211–33 - (online) - Mitchell, Jeffrey. 2021.
Social Trust and Anti-immigrant Attitudes in Europe: A Longitudinal Multi-Level Analysis.
Frontiers in Sociology 6 (April): 604884 - (online) - Akaeda, Naoki. 2023.
Trust and the Educational Gap in the Demand for Redistribution: Evidence from the World Values Survey and the European Value Study.
International Sociology 38(3): 290–310 Library access - Wu, Cary. 2021.
Education and Social Trust in Global Perspective
. Sociological Perspectives 64(6):1166–86. Available here: Library access - Dingemans, Ellen, and Erik Van Ingen. 2015.
Does Religion Breed Trust? A Cross-National Study of the Effects of Religious Involvement, Religious Faith, and Religious Context on Social Trust
. Journal for the Scientific Study of Religion 54(4):739–55. Library access
Further readings
- ARM: Chapters 13 (pp. 279-299), 14 (pp. 301-323) and 15 (pp. 325-342)
A brief review of single-level regression

A brief review of single-level regression

- We aim to model an outcome measurement, our
estimand
: \(\color{green}{Y}\) - We have data on a number \((n)\) of observations \(({i})\) (e.g. survey respondents; pupils; students; factory workers; events; etc.): \({i}_{1\dots{n}}\)
- We assume that observations are independent of each other (e.g. different respondents randomly sampled from a population)
- The outcome measurement has a grand mean across all observations \((\mu)\), and each observation \((i)\) has some deviation (
error
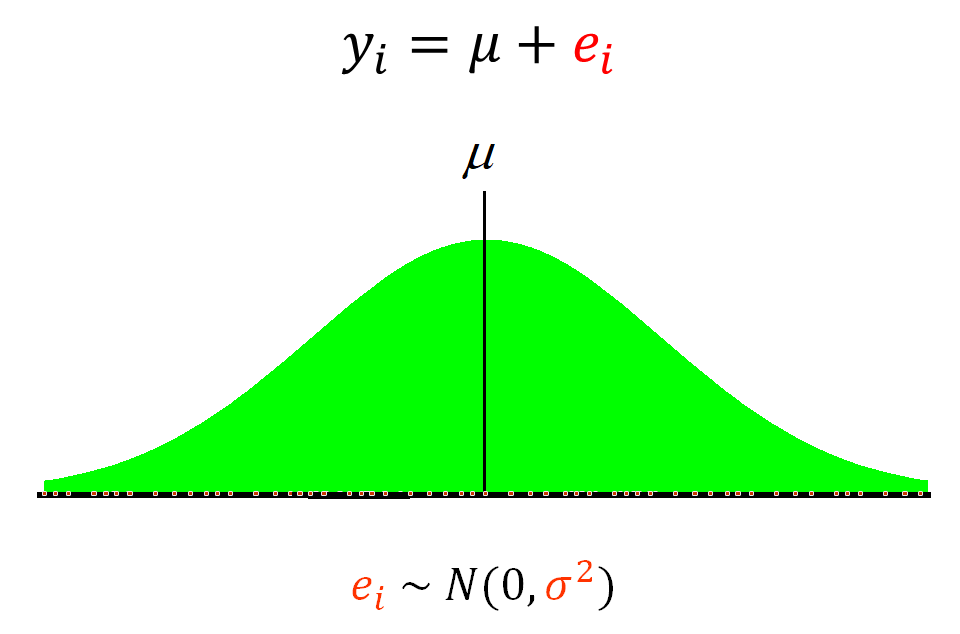
) from this mean \((e_i)\) - \[ y_i = \mu + \color{red}{e_i} \]
A brief review of single-level regression
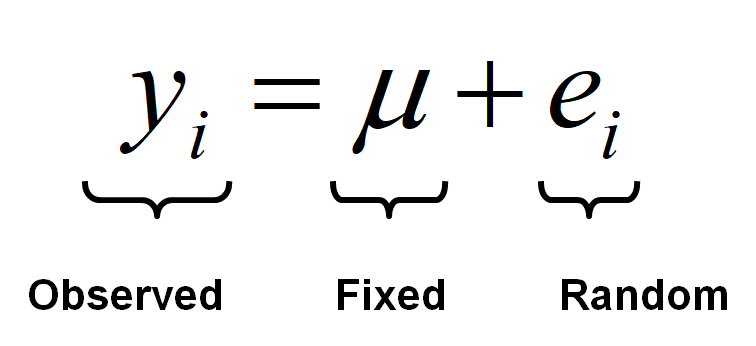
Observed part: our observation, outcome, estimate, etc.; the left-hand-side of the model
Fixed part: this can be a simple sample mean \((\mu)\) of a single measurement as in our basic example (e.g. a social trust scale), but it can also be a regression equation containing several predictor variables, as we have seen in previous weeks (e.g. \(b_0 + b_{1i}x_{1i} + b_{2i}x_{2i} \cdots b_{pi}x_{pi}\) for a model with \(p\) number of predictors/independent variables)
Random part: the deviations of the observations from the model mean
A brief review of single-level regression
- We also assume that the error term \((e)\) is Normally distributed around a mean of 0 and has some variance \((\sigma^2)\) that we are estimating
Multilevel models

Multilevel models: terminology
The terminology surrounding multilevel models can be confusing. Different disciplines use various names for them, for example:
- Variance components
- Random intercepts and slopes
- Random effects
- Random coefficients
- Varying coefficients
- Intercepts- and/or slopes-as-outcomes
- Hierarchical linear models
- Multilevel models (implies multiple levels of hierarchically clustered data)
- Growth curve models (possibly Latent GCM)
- Mixed effects models
Multilevel models: terminology
The terminology surrounding multilevel models can be confusing. Different disciplines use various names for them, for example:
- Variance components
- Random intercepts and slopes
- Random effects
- Random coefficients
- Varying coefficients
- Intercepts- and/or slopes-as-outcomes
- Hierarchical linear models
- Multilevel models (implies multiple levels of hierarchically clustered data)
- Growth curve models (possibly Latent GCM)
- Mixed effects models
Multilevel models: terminology
Some of these terms might be more historical, others are more often seen in a specific discipline, others might refer to a certain data structure, and still others are special cases (e.g. null
models with no explanatory variables).
Random effects are simply those specific to an observational unit, however defined. In our examples We will mostly encounter the case where the observational unit is the level of some grouping factor, but this is only one possibility.
Mixed effects - or simply mixed
- models generally refer to a mixture of fixed and random effects. This is probably the most general term, with no specific data structure implied.
Multilevel data
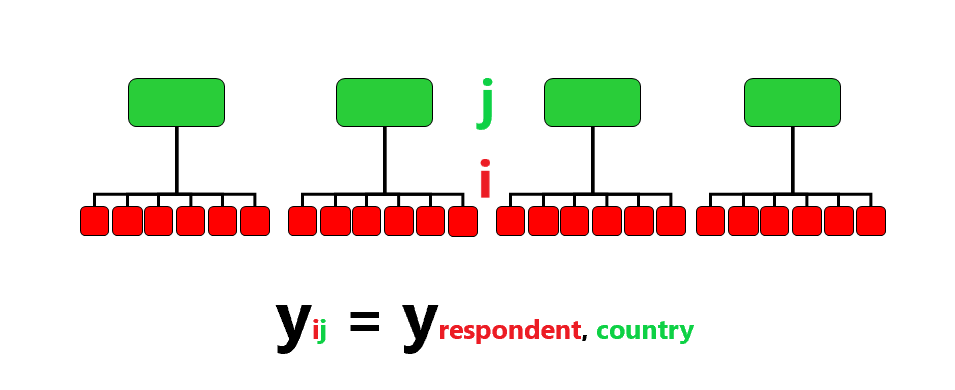
In our dataset we cannot assume that the observations are fully independent (or that the errors are independently distributed). We know that observations were sampled from within selected countries, so the countries are cluster variables that may have a group-level influence on the behaviour, opinions, conditions etc. of our individual observations.
Multilevel data
In our dataset we cannot assume that the observations are fully independent (or that the errors are independently distributed). We know that observations were sampled from within selected countries, so the countries are cluster variables that may have a group-level influence on the behaviour, opinions, conditions etc. of our individual observations.
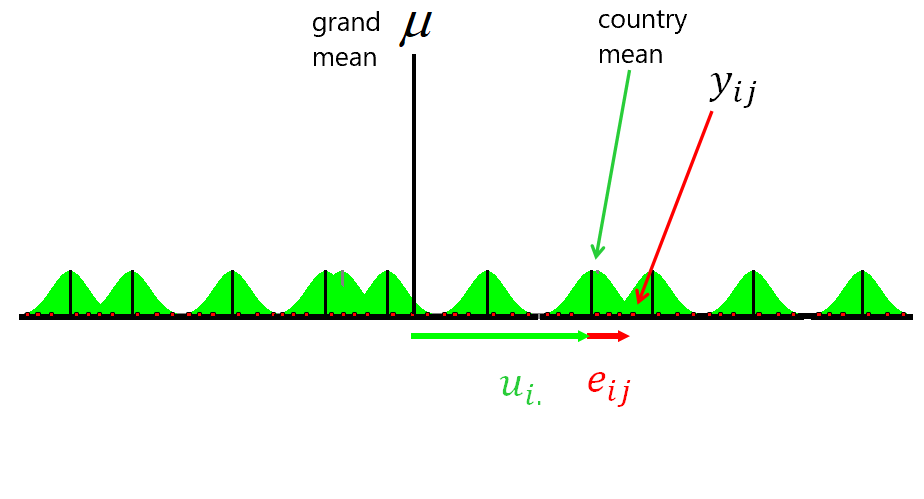
Multilevel data
In our dataset we cannot assume that the observations are fully independent (or that the errors are independently distributed). We know that observations were sampled from within selected countries, so the countries are cluster variables that may have a group-level influence on the behaviour, opinions, conditions etc. of our individual observations.
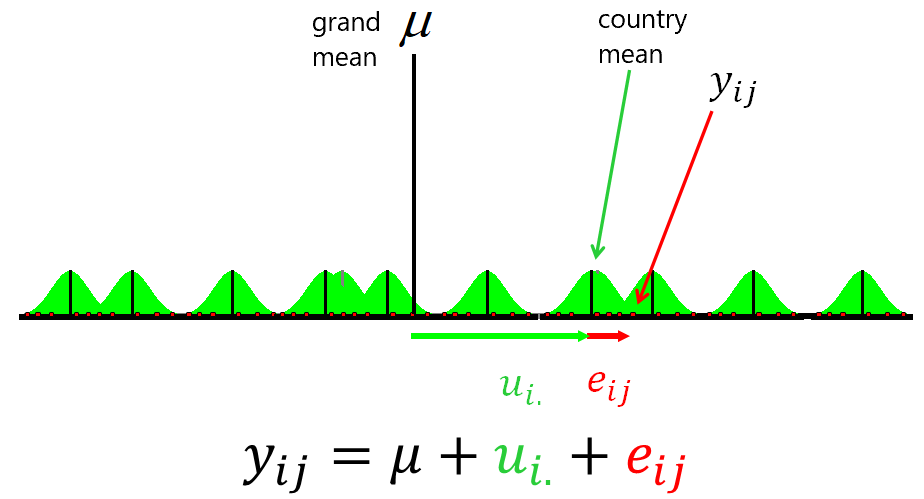
Multilevel data
In our dataset we cannot assume that the observations are fully independent (or that the errors are independently distributed). We know that observations were sampled from within selected countries, so the countries are cluster variables that may have a group-level influence on the behaviour, opinions, conditions etc. of our individual observations.
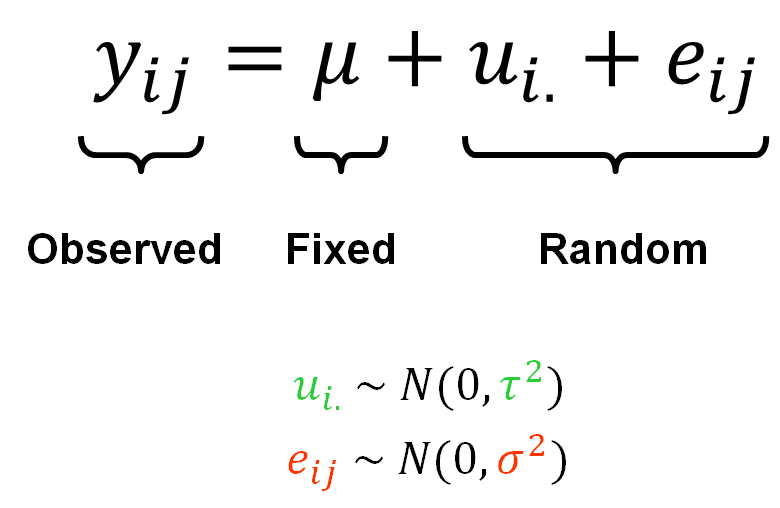
Random intercepts and random effects
Application: Österman (2021)

Application: Österman (2021)
Data from the Österman (2021) article Can We Trust Education for Fostering Trust? Quasi-experimental Evidence on the Effect of Education and Tracking on Social Trust
:
cumulative European Social Survey (ESS) data: nine survey rounds (2002 to 2018)
data are weighted using ESS design weights (we will disregard this, so we can expect our results to differ somewhat)
follows
the established approach of using a validated three-item scale
to study generalised social trust
Application: Österman (2021)
The outcome variable of interest is an eleven-point scale measure of social trust
:
-
The scale consists of the classic trust question, an item on whether people try to be fair, and an item on whether people are helpful:
Generally speaking, would you say that most people can be trusted, or that you can’t be too careful in dealing with people?
-
Do you think that most people would try to take advantage of you if they got the chance, or would they try to be fair?
Would you say that most of the time people try to be helpful or that they are mostly looking out for themselves?
All of the items may be answered on a scale from 0 to 10 (where 10 represents the highest level of trust) and the scale is calculated as the mean of the three items
The three-item scale improves measurement reliability and cross-country validity compared to using a single item, such as the classic trust question.
Application: Österman (2021)
Let’s reduce the dataset for the purpose of our demonstrations to make it run faster:
Application: Österman (2021)
Our dataset looks like this:
| Variable | Mean | SD | IQR | Min | Max | Skewness | Kurtosis | n | n_Missing |
|---|---|---|---|---|---|---|---|---|---|
| cntry | 4.50 | 2.29 | 4.50 | 1.00 | 8.00 | 0.00 | -1.24 | 400 | 0 |
| dweight | 0.99 | 0.41 | 0.39 | 0.03 | 4.34 | 1.77 | 12.12 | 400 | 0 |
| ppltrst | 4.72 | 2.25 | 3.00 | 0.00 | 10.00 | -0.24 | -0.40 | 400 | 0 |
| pplfair | 5.31 | 2.14 | 3.00 | 0.00 | 10.00 | -0.51 | -0.06 | 398 | 2 |
| pplhlp | 4.63 | 2.29 | 3.00 | 0.00 | 10.00 | -0.16 | -0.60 | 399 | 1 |
| eduyrs25 | 12.63 | 4.20 | 6.00 | 0.00 | 24.00 | -7.62e-03 | -0.08 | 395 | 5 |
| paredu_a_high | 1.32 | 0.47 | 1.00 | 1.00 | 2.00 | 0.75 | -1.44 | 379 | 21 |
| trustindex3 | 4.89 | 1.79 | 2.33 | 0.00 | 9.00 | -0.49 | -0.03 | 400 | 0 |
| reform1_7 | 0.46 | 0.50 | 1.00 | 0.00 | 1.00 | 0.15 | -1.99 | 400 | 0 |
| reform_id_num | 14.16 | 6.63 | 12.25 | 4.00 | 26.00 | 0.18 | -0.98 | 400 | 0 |
| female | 1.54 | 0.50 | 1.00 | 1.00 | 2.00 | -0.15 | -1.99 | 400 | 0 |
| agea | 52.49 | 12.89 | 18.00 | 25.00 | 80.00 | -0.37 | -0.51 | 400 | 0 |
| fbrneur | 1.03 | 0.16 | 0.00 | 1.00 | 2.00 | 5.80 | 31.80 | 400 | 0 |
| mbrneur | 1.02 | 0.16 | 0.00 | 1.00 | 2.00 | 6.11 | 35.48 | 400 | 0 |
| fnotbrneur | 1.01 | 0.10 | 0.00 | 1.00 | 2.00 | 9.89 | 96.22 | 400 | 0 |
| mnotbrneur | 1.00 | 0.07 | 0.00 | 1.00 | 2.00 | 14.09 | 197.48 | 400 | 0 |
| blgetmg_d | 1.01 | 0.11 | 0.00 | 1.00 | 2.00 | 8.81 | 75.97 | 400 | 0 |
| yrbrn | 1957.84 | 12.66 | 13.00 | 1927.00 | 1992.00 | 0.60 | 0.04 | 400 | 0 |
| essround | 4.94 | 2.42 | 4.00 | 1.00 | 9.00 | 0.02 | -1.12 | 400 | 0 |
Application: Österman (2021)
The country
variable
| Country (osterman$cntry) (character) | ||||
|---|---|---|---|---|
| Value | N | Raw % | Valid % | Cumulative % |
| DE | 50 | 12.50 | 12.50 | 12.50 |
| ES | 50 | 12.50 | 12.50 | 25.00 |
| FR | 50 | 12.50 | 12.50 | 37.50 |
| GB | 50 | 12.50 | 12.50 | 50.00 |
| HU | 50 | 12.50 | 12.50 | 62.50 |
| IE | 50 | 12.50 | 12.50 | 75.00 |
| PL | 50 | 12.50 | 12.50 | 87.50 |
| PT | 50 | 12.50 | 12.50 | 100.00 |
| (NA) | 0 | 0.00 | (NA) | (NA) |
| total N=400 valid N=400 | ||||
Application: Österman (2021)
In our dataset we cannot assume that the observations are fully independent (or that the errors are independently distributed). We know that observations were sampled from within selected countries, so the countries are cluster variables that may have a group-level influence on the behaviour, opinions, conditions etc. of our individual observations.
With such data, it makes sense to allow regression coefficients to vary by group.
Such variation can already be achieved by simply including group indicators in a least squares regression framework.
In other words, we could extend our previous model like such:
\[trustindex3=\beta_0+\beta_1*eduyears25+\beta_2*agea+\beta_3*female+\\ +\beta_4*{paredu}+\beta_5*{fmnoncntr}+\color{red}{\beta_6*{cntry}}+error\]
Application: Österman (2021)
Let’s start by fitting a single-level model of social trust as a function of education, age, gender, parental education and whether either of the parents were born abroad (i.e. the variable we computed earlier).
Mathematically, we fit the following model:
\[trustindex3=\beta_0+\beta_1*eduyears25+\beta_2*agea+\beta_3*female+\\ +\beta_4*{paredu}+\beta_5*{fmnoncntr}+error\]
Application: Österman (2021)
Model summary:
| Observations | 400 |
| Dependent variable | trustindex3 |
| Type | OLS linear regression |
| F(75,324) | 1.540 |
| R² | 0.263 |
| Adj. R² | 0.092 |
| Est. | 2.5% | 97.5% | t val. | p | |
|---|---|---|---|---|---|
| (Intercept) | 29469.846 | -12688.876 | 71628.568 | 1.375 | 0.170 |
| reform1_7 | 0.025 | -0.757 | 0.807 | 0.063 | 0.950 |
| femaleFemale | -0.024 | -0.406 | 0.358 | -0.124 | 0.901 |
| blgetmg_dYes | -0.899 | -2.605 | 0.806 | -1.037 | 0.300 |
| fbrneurYes | -1.060 | -2.403 | 0.283 | -1.552 | 0.122 |
| mbrneurYes | 0.169 | -1.204 | 1.542 | 0.242 | 0.809 |
| fnotbrneurYes | 0.225 | -2.459 | 2.910 | 0.165 | 0.869 |
| mnotbrneurYes | 0.347 | -3.405 | 4.100 | 0.182 | 0.856 |
| factor(essround)2 | 0.971 | -0.307 | 2.250 | 1.495 | 0.136 |
| factor(essround)3 | 2.076 | 0.116 | 4.035 | 2.084 | 0.038 |
| factor(essround)4 | 3.129 | 0.294 | 5.964 | 2.171 | 0.031 |
| factor(essround)5 | 4.097 | 0.395 | 7.799 | 2.177 | 0.030 |
| factor(essround)6 | 5.022 | 0.417 | 9.627 | 2.145 | 0.033 |
| factor(essround)7 | 6.382 | 0.897 | 11.868 | 2.289 | 0.023 |
| factor(essround)8 | 7.511 | 1.205 | 13.817 | 2.343 | 0.020 |
| factor(essround)9 | 7.815 | 0.485 | 15.146 | 2.097 | 0.037 |
| agea | 0.539 | -0.705 | 1.784 | 0.853 | 0.395 |
| yrbrn | -29.589 | -72.854 | 13.677 | -1.345 | 0.179 |
| I(agea^2) | -0.010 | -0.020 | 0.000 | -1.931 | 0.054 |
| I(yrbrn^2) | 0.007 | -0.004 | 0.019 | 1.316 | 0.189 |
| factor(reform_id_num)7 | 662.225 | -595.549 | 1919.999 | 1.036 | 0.301 |
| factor(reform_id_num)8 | -203.414 | -781.354 | 374.526 | -0.692 | 0.489 |
| factor(reform_id_num)10 | 61.107 | -845.801 | 968.016 | 0.133 | 0.895 |
| factor(reform_id_num)11 | -609.828 | -1232.251 | 12.595 | -1.928 | 0.055 |
| factor(reform_id_num)12 | -772.168 | -2067.215 | 522.879 | -1.173 | 0.242 |
| factor(reform_id_num)13 | -92.291 | -665.155 | 480.574 | -0.317 | 0.751 |
| factor(reform_id_num)15 | -396.977 | -875.659 | 81.705 | -1.632 | 0.104 |
| factor(reform_id_num)16 | 143.466 | -451.642 | 738.574 | 0.474 | 0.636 |
| factor(reform_id_num)17 | 1131.943 | -433.067 | 2696.954 | 1.423 | 0.156 |
| factor(reform_id_num)22 | -523.281 | -1013.983 | -32.579 | -2.098 | 0.037 |
| factor(reform_id_num)23 | -80.618 | -1716.372 | 1555.136 | -0.097 | 0.923 |
| factor(reform_id_num)24 | -414.652 | -1069.579 | 240.275 | -1.246 | 0.214 |
| factor(reform_id_num)25 | -69.812 | -783.036 | 643.413 | -0.193 | 0.847 |
| factor(reform_id_num)26 | 978.626 | -439.588 | 2396.841 | 1.358 | 0.176 |
| yrbrn:factor(reform_id_num)7 | -0.338 | -0.971 | 0.295 | -1.051 | 0.294 |
| yrbrn:factor(reform_id_num)8 | 0.127 | -0.161 | 0.415 | 0.866 | 0.387 |
| yrbrn:factor(reform_id_num)10 | -0.008 | -0.465 | 0.449 | -0.033 | 0.973 |
| yrbrn:factor(reform_id_num)11 | 0.330 | 0.019 | 0.640 | 2.090 | 0.037 |
| yrbrn:factor(reform_id_num)12 | 0.465 | -0.188 | 1.119 | 1.401 | 0.162 |
| yrbrn:factor(reform_id_num)13 | 0.055 | -0.234 | 0.345 | 0.375 | 0.708 |
| yrbrn:factor(reform_id_num)15 | 0.211 | -0.036 | 0.457 | 1.679 | 0.094 |
| yrbrn:factor(reform_id_num)16 | -0.066 | -0.368 | 0.236 | -0.430 | 0.667 |
| yrbrn:factor(reform_id_num)17 | -0.558 | -1.348 | 0.233 | -1.388 | 0.166 |
| yrbrn:factor(reform_id_num)22 | 0.270 | 0.021 | 0.520 | 2.129 | 0.034 |
| yrbrn:factor(reform_id_num)23 | 0.060 | -0.766 | 0.887 | 0.143 | 0.886 |
| yrbrn:factor(reform_id_num)24 | 0.219 | -0.130 | 0.567 | 1.235 | 0.218 |
| yrbrn:factor(reform_id_num)25 | 0.065 | -0.300 | 0.430 | 0.350 | 0.726 |
| yrbrn:factor(reform_id_num)26 | -0.471 | -1.186 | 0.243 | -1.297 | 0.196 |
| agea:factor(reform_id_num)7 | 0.915 | -1.245 | 3.074 | 0.833 | 0.405 |
| agea:factor(reform_id_num)8 | -1.804 | -3.534 | -0.074 | -2.052 | 0.041 |
| agea:factor(reform_id_num)10 | -2.040 | -3.952 | -0.127 | -2.098 | 0.037 |
| agea:factor(reform_id_num)11 | -1.427 | -3.651 | 0.798 | -1.262 | 0.208 |
| agea:factor(reform_id_num)12 | -4.062 | -11.167 | 3.044 | -1.125 | 0.262 |
| agea:factor(reform_id_num)13 | -0.652 | -2.368 | 1.065 | -0.747 | 0.456 |
| agea:factor(reform_id_num)15 | -0.723 | -2.247 | 0.800 | -0.934 | 0.351 |
| agea:factor(reform_id_num)16 | -0.502 | -1.936 | 0.932 | -0.689 | 0.492 |
| agea:factor(reform_id_num)17 | -1.352 | -5.243 | 2.539 | -0.684 | 0.495 |
| agea:factor(reform_id_num)22 | -0.475 | -1.904 | 0.955 | -0.654 | 0.514 |
| agea:factor(reform_id_num)23 | -2.400 | -5.442 | 0.643 | -1.551 | 0.122 |
| agea:factor(reform_id_num)24 | -0.660 | -8.127 | 6.807 | -0.174 | 0.862 |
| agea:factor(reform_id_num)25 | -2.230 | -5.582 | 1.121 | -1.309 | 0.191 |
| agea:factor(reform_id_num)26 | -2.386 | -5.812 | 1.040 | -1.370 | 0.172 |
| I(agea^2):factor(reform_id_num)7 | -0.021 | -0.049 | 0.007 | -1.453 | 0.147 |
| I(agea^2):factor(reform_id_num)8 | 0.018 | 0.002 | 0.034 | 2.204 | 0.028 |
| I(agea^2):factor(reform_id_num)10 | 0.022 | 0.002 | 0.042 | 2.162 | 0.031 |
| I(agea^2):factor(reform_id_num)11 | 0.014 | -0.005 | 0.034 | 1.443 | 0.150 |
| I(agea^2):factor(reform_id_num)12 | 0.032 | -0.018 | 0.081 | 1.255 | 0.210 |
| I(agea^2):factor(reform_id_num)13 | 0.007 | -0.009 | 0.022 | 0.834 | 0.405 |
| I(agea^2):factor(reform_id_num)15 | 0.008 | -0.005 | 0.021 | 1.223 | 0.222 |
| I(agea^2):factor(reform_id_num)16 | 0.005 | -0.009 | 0.018 | 0.680 | 0.497 |
| I(agea^2):factor(reform_id_num)17 | 0.017 | -0.044 | 0.077 | 0.536 | 0.592 |
| I(agea^2):factor(reform_id_num)22 | 0.006 | -0.006 | 0.019 | 0.992 | 0.322 |
| I(agea^2):factor(reform_id_num)23 | 0.035 | -0.011 | 0.081 | 1.509 | 0.132 |
| I(agea^2):factor(reform_id_num)24 | 0.008 | -0.053 | 0.068 | 0.244 | 0.808 |
| I(agea^2):factor(reform_id_num)25 | 0.021 | -0.010 | 0.053 | 1.331 | 0.184 |
| I(agea^2):factor(reform_id_num)26 | 0.029 | -0.022 | 0.080 | 1.127 | 0.261 |
| Standard errors: OLS |
We have interpreted this model in earlier weeks. Our interest now is in extending it to account for the nesting of cases within different countries.
Fitting multilevel models
In R we can fit multilevel models using the lmer function from the lme4 package.
Initially, it is advisable to first fit some simple, preliminary models, in part to establish a baseline for evaluating larger models. Then, we can build toward a final model for description and inference by attempting to add important covariates, centring certain variables, and checking model assumptions.
The standard first step is to model only the outcome measurement, without any predictors, to get a sense for the effect of the clusters; this is often called a random intercepts model or null model:
The second step is then to fit the full covariate model:
Fitting multilevel models
Results: null
model:
| Observations | 400 |
| Dependent variable | trustindex3 |
| Type | Mixed effects linear regression |
| AIC | 1590.16 |
| BIC | 1602.13 |
| Pseudo-R² (fixed effects) | 0.00 |
| Pseudo-R² (total) | 0.09 |
Fixed Effects
|
|||||
|---|---|---|---|---|---|
| Est. | S.E. | t val. | d.f. | p | |
| (Intercept) | 4.89 | 0.21 | 23.39 | 7.00 | 0.00 |
| p values calculated using Satterthwaite d.f. | |||||
Random Effects
|
||
|---|---|---|
| Group | Parameter | Std. Dev. |
| cntry | (Intercept) | 0.54 |
| Residual | 1.72 | |
Grouping Variables
|
||
|---|---|---|
| Group | # groups | ICC |
| cntry | 8 | 0.09 |
The intra-class correlation (ICC) tells us the percentage of variation in the outcome variable attributable to differences between countries.
Fitting multilevel models
Results: Covariate model:
| Observations | 400 |
| Dependent variable | trustindex3 |
| Type | Mixed effects linear regression |
| AIC | 1596.38 |
| BIC | 1636.29 |
| Pseudo-R² (fixed effects) | 0.01 |
| Pseudo-R² (total) | 0.09 |
Fixed Effects
|
|||||
|---|---|---|---|---|---|
| Est. | S.E. | t val. | d.f. | p | |
| (Intercept) | 4.99 | 0.24 | 20.80 | 12.58 | 0.00 |
| reform1_7 | -0.08 | 0.18 | -0.44 | 389.73 | 0.66 |
| femaleFemale | -0.06 | 0.18 | -0.33 | 388.45 | 0.74 |
| blgetmg_dYes | -0.31 | 0.78 | -0.40 | 386.04 | 0.69 |
| fbrneurYes | -0.86 | 0.65 | -1.32 | 388.18 | 0.19 |
| mbrneurYes | -0.09 | 0.67 | -0.14 | 386.62 | 0.89 |
| fnotbrneurYes | 0.13 | 1.24 | 0.11 | 387.15 | 0.91 |
| mnotbrneurYes | 0.26 | 1.76 | 0.15 | 388.71 | 0.88 |
| p values calculated using Satterthwaite d.f. | |||||
Random Effects
|
||
|---|---|---|
| Group | Parameter | Std. Dev. |
| cntry | (Intercept) | 0.53 |
| Residual | 1.73 | |
Grouping Variables
|
||
|---|---|---|
| Group | # groups | ICC |
| cntry | 8 | 0.09 |

 for full screen
for full screen