Quantitative analysis

2025

Dr Chris Moreh

Week 8

Conclusions

Sum up, divide, and conquer

Click and press for full screen

View on

Let’s play!

apps.chrismoreh.com/Monty

Take-home exercises

• Play some more before and after this lecture, then download all your data from the app
• Build some plots of the data to address these questions, making some transformations to the dataset if/as required:
  1. How many games have you won in total?
  2. What was your overall win rate?
  3. How often have you switched away from your initial door?
  4. How often did you win when you switched, and how often when you stayed?
• Test the statistical association between switching and winning
• How has your switching behaviour developed over time? Test the association between time (the Timestamp column/variable) and switching choice
• Has your switching behaviour changed between and after the lecture? Test this causal question statistically.

Solutions

1. Simulation
2. Transmutation
3. Enumeration
4. Causal reasoning (graphical model)
5. Bayesian reasoning

Simulation

  n_games           = 1000
  balanced          = FALSE
  
  df_games          = data.frame()
  
  for (i in 1:n_games) {
    winning_door    = sample(c("Door 1", "Door 2", "Door 3"), size = 1)
    original_choice = sample(c("Door 1", "Door 2", "Door 3"), size = 1)
    losing_doors    = setdiff(c("Door 1", "Door 2", "Door 3"), winning_door)
    revealed_door   = ifelse(original_choice == winning_door,
                             sample(losing_doors, size = 1),
                             setdiff(losing_doors, original_choice)
                             )
    switched        = ifelse(balanced,
                             ifelse(i <= n_games/2, "Switched", "Not switched"),
                             sample(c("Switched", "Not switched"), size = 1)
                             )
    final_choice    = ifelse(switched == "Switched", 
                             setdiff(c("Door 1", "Door 2", "Door 3"), c(revealed_door, original_choice)), 
                             original_choice
                             )
    outcome         = ifelse(final_choice == winning_door,
                             "Won",
                             "Lost"
                             )
    
    game            = cbind(game = i,
                            winning_door,
                            original_choice,
                            switched,
                            outcome
                            )
    df_games        = rbind(df_games, 
                            game)
  }

Simulation

  n_games           = 1000
  balanced          = FALSE
  
monty <- function(n_games = 1000, balanced = TRUE) {
  
  df_games          = data.frame()
  
  for (i in 1:n_games) {
    winning_door    = sample(c("Door 1", "Door 2", "Door 3"), size = 1)
    original_choice = sample(c("Door 1", "Door 2", "Door 3"), size = 1)
    losing_doors    = setdiff(c("Door 1", "Door 2", "Door 3"), winning_door)
    revealed_door   = ifelse(original_choice == winning_door,
                             sample(losing_doors, size = 1),
                             setdiff(losing_doors, original_choice)
                             )
    switched        = ifelse(balanced,
                             ifelse(i <= n_games/2, "Switched", "Not switched"),
                             sample(c("Switched", "Not switched"), size = 1)
                             )
    final_choice    = ifelse(switched == "Switched", 
                             setdiff(c("Door 1", "Door 2", "Door 3"), c(revealed_door, original_choice)), 
                             original_choice
                             )
    outcome         = ifelse(final_choice == winning_door,
                             "Won",
                             "Lost"
                             )
    
    game            = cbind(game = i,
                            winning_door,
                            original_choice,
                            switched,
                            outcome
                            )
    df_games        = rbind(df_games, 
                            game)
  }

  return(df_games)
}

Simulation

monty(100) |>
  ggplot(aes(x = switched, fill = outcome)) + 
  geom_bar(position="fill", stat="count") + 
  scale_fill_manual(values = c("#880e0e50", "#396e0a")) + 
  labs(x = "\nDid the player switch their choice?", 
       fill = "Outcome ", y = "Percent (%) of games\n") +
  theme_minimal() +
  theme(legend.position = "top")

Simulation

monty(100) |>
  ggplot(aes(x = switched, fill = outcome)) + 
  geom_bar(position="fill", stat="count") + 
  scale_fill_manual(values = c("#880e0e50", "#396e0a")) + 
  labs(x = "\nDid the player switch their choice?", 
       fill = "Outcome ", y = "Percent (%) of games\n") +
  theme_minimal() +
  theme(legend.position = "top")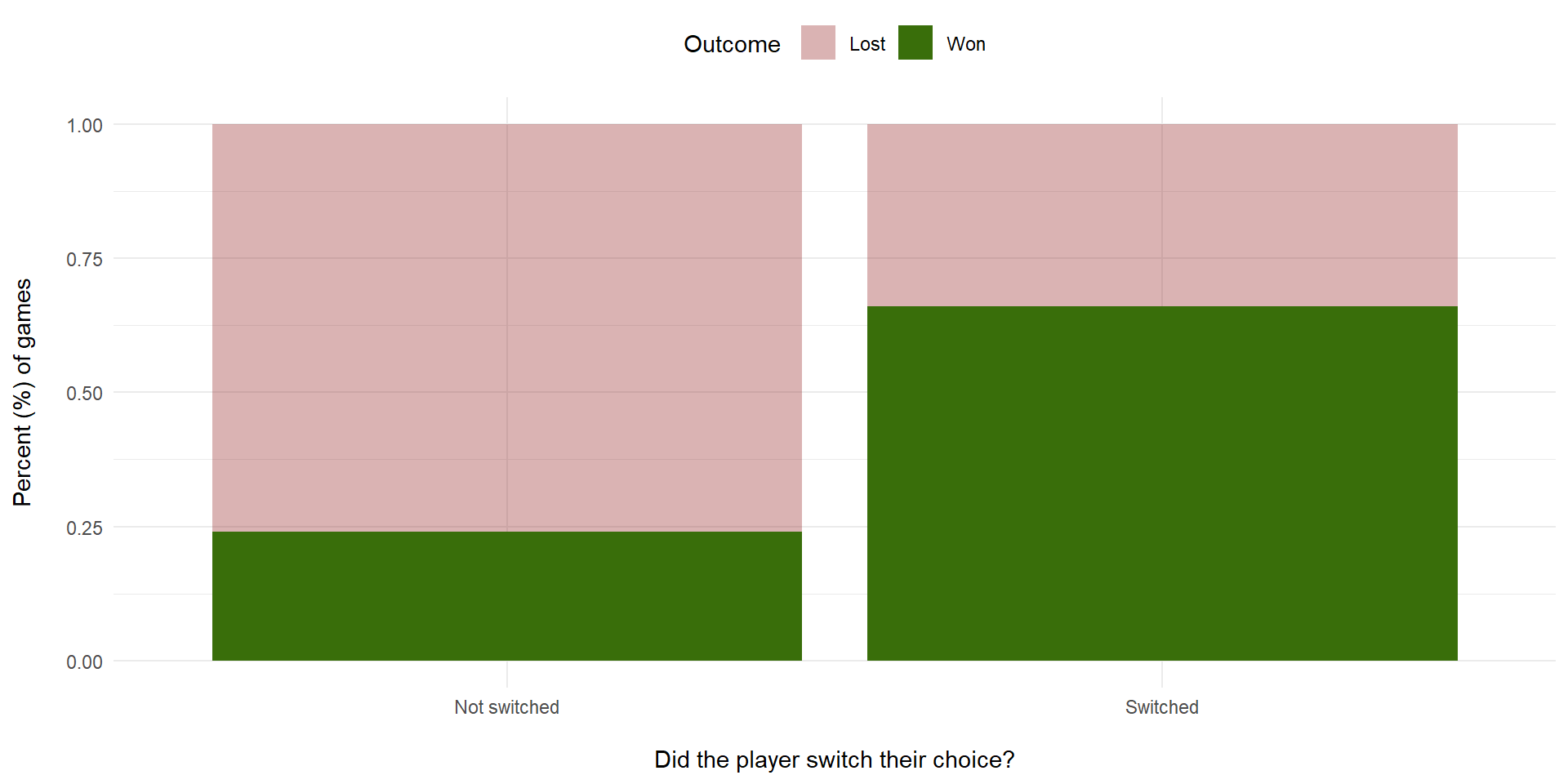

Simulation

plot = list()

for (i in 1:49) {
plot[[i]] <- 
monty(1000) |>
  ggplot(aes(x = switched, fill = outcome)) + 
  geom_bar(position="fill", stat="count") + 
  scale_fill_manual(values = c("#880e0e50", "#396e0a")) + 
  scale_y_continuous(labels = scales::percent_format()) +
  labs(x = NULL, 
       fill = NULL, 
       y = NULL) +
  theme_minimal() +
  theme(legend.position = "none")
}

patchwork::wrap_plots(plot)

Simulation

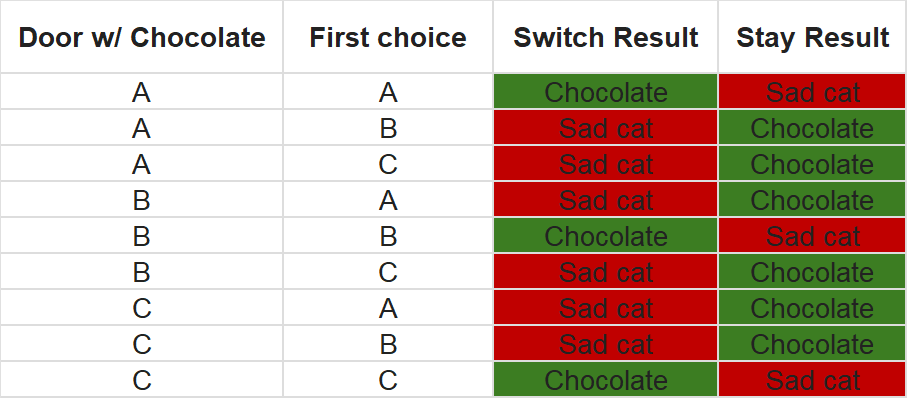
Enumeration

Enumeration

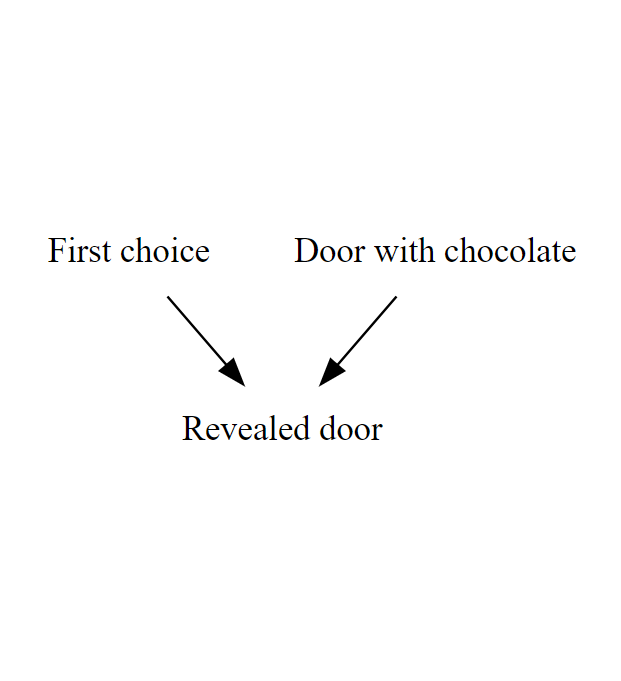
Causal graphs

Bayesian reasoning

• Host could not open Door 1 after you chose it — but he could have opened Door 2.

• The fact that he did not, makes it more likely that he opened Door 3 because he was forced to.

• Thus there is more evidence than before that the prize is behind Door 2.

• Any hypothesis that has survived some test that threatens its validity becomes more likely. The greater the threat, the more likely it becomes after surviving.